10 Soal & Pembahasan Hukum Gravitasi Newton (bagian 2) ǀ Pilihan Ganda - Cuntorio

  

Sebelumnya, kita telah membahas soal hukum Gravitasi Newton (bagian 1). Sekarang, kita akan lanjutkan ke soal dan pembahasan hukum Gravitasi Newton (bagian 2) khusus pilihan ganda.

 

Baca sebelumnya : 10 Soal & Pembahasan Hukum Gravitasi Newton (bagian 1) ǀ Pilihan Ganda

 

Pilihlah jawaban yang tepat dari pilihan di bawah ini.

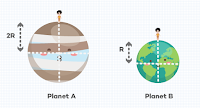
11. Perbandingan jari-jari Planet A dan jari-jari Bumi adalah 2 : 1. Sedangkan, perbandingan massa kedua planet adalah 10 : 1. Jika berat Gading di Bumi adalah 80 N, maka berat Gading di Planet A adalah . . .

   A. 60 N

   B. 100 N

   C. 150 N

   D. 200 N

   E. 250 N

Pembahasan :

Kata “berat” telah mengacu pada makna gaya. Jelas gaya yang dimaksud adalah gaya gravitasi. Jika Gading berada di atas permukaan Bumi atau Planet A, maka jarak antara Gading dengan Bumi atau Gading dengan Planet A adalah jari-jari keduanya.

Diketahui :

F_GB = 80 N

r_GA = 2R

r_GB = 1R

m_A= 10m

m_B = 1m

Ditanya : gaya gravitasi Gading di Planet A (F_{Gading-PlanetA}) atau F_GA

Jika F = (G.m₁.m₂/r₁₂²) maka G = (F. r₁₂²/ m₁.m₂). Nilai G pada dua kondisi di atas adalah sama besar. Oleh karena itu

GGading-PlanetA	=	GGading-Bumi
GGA	=	GGB
FGA. rGA²/ mG.mA	=	FGB. rGB²/ mG.mB
FGA. (2R)²/ (10m)	=	(80).(1R)²/ (1m)
FGA.4R²/ 10	=	80.R²
FGA.4/ 10	=	80
FGA	=	200

Jawaban E

 

12. Jika jari-jari bumi adalah R dan berat benda di permukaan bumi adalah W, maka berat benda tersebut pada ketinggian (1/2) R dari permukaan bumi adalah . . .

   A. 2W/3

   B. 3W/2

   C. W

   D. 4W/9

   E. 9W/4

Pembahasan :

Gaya berat sama dengan gaya gravitasi. Jadi, sebenarnya kita mencari gaya gravitasi. Jarak harus dihitung dari pusat bumi. Jika jarak dihitung dari permukaan Bumi, maka kita harus menambahkan nya dulu dengan jari-jari Bumi.

GBumi-Benda saat R	=	GBumi-Benda saat R+0,5R
GBB saat R	=	GBB saat 1,5R
FBP. rBB²/ mB.mB	=	FBB’. rBB’²/ mB.mB
FBP. rBB²	=	FBB’. rBB’²
W. (R)²	=	FBB’.(1,5R)²
W. R²	=	FBB’. 2,25R²
W	=	FBB’. (9/4)
FBB’	=	(4/9)W

Jawaban D

 

13. Berat astronot di bumi adalah 800 N. Astronot tersebut kemudian naik pesawat meninggalkan bumi hingga mengorbit pada ketinggian R (R = jari-jari bumi = 6380 km). Jika besar konstanta gravitasi 6,67 x 10-11 Nm²kg², maka berat astronot pada orbit tersebut adalah . . .

   A. 200 N

   B. 220 N

   C. 240 N

   D. 260 N

   E. 280 N

Pembahasan :

Gaya berat sama dengan gaya gravitasi. Jadi, sebenarnya kita mencari gaya gravitasi

GOrang- Bumi saat R	=	GOrang- Bumi saat R+R
GBB saat R	=	GBB saat 2R
FBP. rBB²/ mB.mB	=	FBB’. rBB’²/ mB.mB
FBP. rBB²	=	FBB’. rBB’²
(800). (R)²	=	FBB’.(2R)²
800. R²	=	FBB’. 4R²
800	=	FBB’.4
FBB’	=	200

Jawaban A.

 

14. Jika percepatan gravitasi di permukaan bumi adalah 10 m/s², maka besar percepatan gravitasi pada ketinggian 3R dari pusat bumi adalah . . .

   A. 1,1 m/s²

   B. 1,9 m/s²

   C. 2,0 m/s²

   D. 2,1 m/s²

   E. 3,0 m/s²

Pembahasan :

Percepatan gravitasi disebut juga kuat medan gravitasi (g). Kita perlu mencari nilai g pada jarak 3R dari pusat bumi. Jarak sudah tepat diukur dari pusat bumi, sehingga kita tidak perlu menambahnya dengan R. Persamaan percepatan gravitasi bumi adalah g = G.m_Bumi/r_Bumi²

*Kuat medan gravitasi (g_Bumi-Benda atau g_BB)

g_BB = G.m_Bumi /r²

G = g_BB.r²/m_Bumi

*Mencari nilai g saat r = 3R

GBumi saat R	=	GBumi saat 3R
GB saat R	=	GB saat 4R
gB.r2/mBumi	=	gB’.r’2/mBumi
gB.r2	=	gB’.r’2
10.R²	=	gB’.(3R)²
10.R²	=	gB’.9R²
10	=	gBB’.9
gBB	=	10/9
gBB	=	1,1

Jawaban A.

 

15. Benda mengalami percepatan gravitasi sebesar 6 m/s² di permukaan planet A. Jika massa planet adalah 3,6 x 10²¹ kg, maka percepatan gravitasi yang akan dialami benda pada ketinggian 100 km di atas permukaan planet tersebut adalah . . .

   A. 2,7 m/s²

   B. 3,7 m/s²

   C. 1,4 m/s²

   D. 3,2 m/s²

   E. 2,9 m/s²

Pembahasan :

Diketahui :

g_A = 6 m/s²

G = 6,674 x 10^-11 m³/kg.s²

m_A = 3,6 x 10²¹

r = r

r’ = (100 km) + r = (1 x 10⁵) m + r

Ditanya : kuat medan gravitasi saat ketinggian 100 km dari permukaan planet (g’)

*Mencari nilai jari-jari (r) Planet A dari nilai g

g_A = G.m_A /r²

r² = G.m_P/ g_A

r² = (6,674 x 10^-11).(3,6 x 10²¹) / 6

r² = (6,674 x 10^-11).(3,6 x 10²¹) / 6

r² = (4,004 x 10¹⁰)

r = (2,0 x 10⁵) m

*Mencari nilai gravitasi g kondisi dua yaitu, saat r’ = (1 x 10⁵) + (2,0 x 10⁵) = 3,0 x 10⁵ m

g_A' = G.m_P /r’²

g_A' = (6,674 x 10^-11).(3,6 x 10²¹) / (3,0 x 10⁵)²

g_A' = (6,674 x 10^-11).(3,6 x 10²¹) / (9 x 10¹⁰)

g_A' = 2,7 m/s²

Jawaban A.

 

16. Perbandingan massa planet A dan B adalah 2 : 3, sedangkan perbandingan jari-jari planet A dan B adalah 1 : 2. Jika berat benda di planet A adalah W, maka berat benda di planet B adalah . . .

   A. 3W/8

   B. 3W/4

   C. W/2

   D. 4W/3

   E. 9W/16

Pembahasan :

Gaya berat sama dengan gaya gravitasi. Jadi, sebenarnya kita mencari gaya gravitasi

Diketahui :

A = Planet A; B = Planet B; B’ = Benda

m_A = 2m ; m_B = 3m

r_AB’ = R ; r_BB’ = 2R

F_AB’ = W

Ditanya : gaya gravitasi benda di permukaan Planet B (F_BB’)

GPlanet A - Benda	=	GPlanet B-Benda
GAB’	=	GBB’
FAB’. rAB’²/ mA.mB’	=	FBB’. rBB’²/ mB.mB’
FAB. rAB’²/ mA	=	FBB’. rBB’²/ mB
W. R²/ 2m	=	FBB’.(2R)²/ 3m
W. R²/ 2	=	FBB’.4R²/ 3
W/ 2	=	FBB’.4/ 3
FBB’	=	(3/8)W

Jawaban A.

 

17. Tiga benda yaitu P, Q, dan R yang masing-masing bermassa 1 kg, 2 kg, dan 4 kg diletakkan pada sudut segitiga siku-siku. Sisi-sisi segitiga tersebut adalah 5 cm, 12 cm, dan 13 cm. Jika Q berada pada sudut siku-siku nya, sedangkan P terletak pada sisi yang paling dekat dengan Q. Besar resultan gaya gravitasi yang dialami benda Q adalah . . .

   A. 2,99 x 10² N

   B. 4,54 x 10^-12 N

   C. 6,50 x 10^-8 N

   D. 1,22 x 10⁹ N

   E. 1,07 x 10^-10 N

Pembahasan :

Pada kondisi ini, Q ditarik P dan R. Jika digambarkan dengan vektor, resultan vektornya akan seperti ini.

Diketahui :

m_P = 1 kg; m_Q = 2 kg; m_R = 4 kg

r_QP = 5 cm = 5 x 10^-2 m

r_QR = 12 cm = 12 x 10^-2 m

G = 6,674 x 10^-11 m³/kg.s²

F_Resultan = √(F_QP² + F_QR²)

Ditanya : resultan gaya (F_Resultan)

*Gaya Q terhadap P (F_QP)

F_QP = G. m_Q. m_P/ r_QP²

F_QP = (6,674 x 10^-11)(2)(1)/ (5 x 10^-2)²

F_QP = (6,674 x 10^-11)(2)(1)/ (25 x 10^-4)

F_QP = (6,674 x 10^-11)(2)(1)/ (25 x 10^-4)

F_QP = (0,534 x 10^-7) N

 

*Gaya Q terhadap R (F_QR)

F_QP = G. m_Q. m_R/ r_QR²

F_QP = (6,674 x 10^-11)(2)(4)/ (12 x 10^-2)²

F_QP = (6,674 x 10^-11)(8)/ (144 x 10^-4)

F_QP = (0,371 x 10^-7) N

 

*Resultan gaya (F_Resultan)

F_Resultan = √(F_QP² + F_QR²)

F_Resultan = √((0,534 x 10^-7)² + (0,371 x 10^-7)²)

F_Resultan = √((0,423 x 10^-14)

F_Resultan = (0,650 x 10^-7)

F_Resultan = (6,50 x 10^-8) N

Jawaban C.

 

18. Bola A dan B memiliki massa sama besar dengan garis tengah juga sama.

Jika kuat medan gravitasi di suatu titik sama dengan nol, maka jarak titik tersebut dari kulit bola A adalah . . .

   A. 2,8 m

   B. 3,5 m

   C. 0,5 m

   D. 2,5 m

   E. 3,0 m

Pembahasan :

Karena benda sama besar dan titik P memiliki kuat medan gravitasi nol. Titik P pasti berada di antara kedua benda dengan jarak sama panjang antara AP dan PB. Jarak AP = jari-jari A + (jarak AB/2) = 0,5 + 2,5 = 3,0 m

Jawaban E.

 

19. Dua benda masing-masing bermassa 2 kg dan 12,5 kg terpisah pada jarak 7 m. Agar gaya gravitasi yang dialami bola bermassa 6 kg sama dengan nol, maka benda harus diletakkan pada jarak . . .

   A. 2 m dari massa 2 kg

   B. 3 m dari massa 2 kg

   C. 4 m dari massa 2 kg

   D. 5 m dari massa 2 kg

   E. 2 m dari massa 12,5 kg

Pembahasan :

Diketahui :

m₁ = 2 kg

m₂ = 12,5 kg

r_1p = x

r₁₂ = d = 7 m

r_2p = d – x = 7 - x

* Jarak benda P ke massa 1 (m₁)

F1P	=	F2P
G. m1.mP/ r1P²	=	G. m2.mP/ r2P²
m1/ r1P²	=	m2/ r2P²
2/ x²	=	(12,5)/ (7 - x)²
(7 - x)²/ x²	=	(12,5)/2
(7 – x)/x	=	√(6,25)
(7 – x)/x	=	2,5
7 - x	=	2,5x
7	=	3,5x
x	=	2

Jadi, jarak pusat benda 1 bermassa 2 kg ke titik P adalah 2 m.

Jawaban A.

 

20. Jika perbandingan jari-jari bumi di khatulistiwa dan di Kutub adalah 9 : 8, maka perbandingan percepatan gravitasi bumi di khatulistiwa dan di Kutub adalah . . .

   A. 1 : 2

   B. 2 : 5

   C. 3 : 2

   D. 81 : 64

   E. 64 : 81

Pembahasan :

*Mencari nilai perbandingan g_khatulistiwa/ g_kutub

GBumi saat R	=	GBumi saat 3R
gkh.rkh2/mBumi	=	gkb.rkb2/mBumi
gkh.rkh2	=	gkb.rkb2
gkh /gkb	=	rkb2 /rkh2
gkh /gkb	=	(8R)2 /(9R)2
gkh /gkb	=	64/ 81

Jawaban E.

 

Baca selanjutnya : 10 Soal & Pembahasan Hukum Gravitasi Newton (bagian 3) ǀ Pilihan Ganda

 

Itulah 10 soal dan pembahasan hukum Gravitasi Newton (bagian 2). Klik selanjutnya untuk melihat pembahasan lainnya.